Which Triangle Congruence Theorem Could Be Used to Show
In the above figure Δ ABC and Δ PQR are congruent triangles. 20 Questions Show answers.
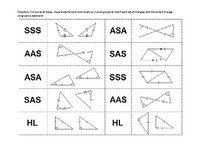
Triangle Congruence Theorems Algebra I Quizizz
1 point Which construction is illustrated above.
. AAS Triangle Congruence Theorem B. Which congruence theorem can be used to prove that the triangles are congruent. This principle is known as Hypotenuse-Acute Angle theorem.
B and E are right angles. 1 Since 1 and 2 are vertically opposite angles so they must be equal. The SAS rule states that.
To play this quiz please finish editing it. O a perpendicular to a given line at a point on the line O an angle congruent to a given angle O the bisector. This means ABE is an isosceles triangle.
Side-Angle-Side is a rule used to prove whether a given set of triangles are congruent. Repeat parts ae several times redrawing A in different orientations. Hence sides BC and AD View the full answer.
Use the same angle measure for A the same radius for the circle and the same angle. An included angle is an angle formed by two given sides. A polygon made of three line segments forming three angles is known as a Triangle.
Because of CPCTC segment AC is congruent to segment. Which triangle congruence theorem can be used to prove the triangles are congruent. The correct options are B SAS B ECA and D AC.
Corresponding sides g and b are congruent. HUG and LAB each have one angle measuring exactly 63. Therefore in both the triangles two pairs of corresponding sides and the angle included between them are congruent.
What triangle congruency theorem can be used. If two sides and the included angle of one triangle are equal to two sides and included angle of another triangle then the triangles are congruent. Solution for What theorem can be used to show that ABC DEF.
Sss triangle congruence theorem could be used to show triangle ABC CDA. Which triangle congruence theorem could be used to immediately show ABC ADBC with no additional steps. SSS Triangle Congruence Theorem C.
We use the symbol to show congruence. Corresponding sides and angles mean that the side on one triangle and the side on the other triangle in the same position match. Which triangle congruence theorem can be used to prove the triangles are congruent.
56 Proving Triangle Congruence by ASA and AAS 259 Construct Arguments When two triangles have four pairs of congruent corresponding parts can you conclude that the triangles are congruent. Thus two triangles can be superimposed side to side and angle to angle. In a parallelogram opposite sides are congruent.
To prove the triangles are congruent. Two triangles are congruent if their corresponding sides are equal in length and their corresponding interior angles are equal in measure. A D с OSAS O ASA OHL OSSS 13.
The explanations are given one by one as follows. The SAS Postulate tells us If two sides and the included angle of a triangle are congruent to two sides and the included angle of another triangle then the two triangles are congruent. Two triangles are said to be congruent if their sides have the same length and angles have same measure.
We can then determine ABC AED by. This quiz is incomplete. Triangle Congruence and Two Column Proofs.
Two angles and the non-included side of one triangle are congruent to the corresponding parts of another triangle. Geometry questions and answers. Triangle ACD is an isosceles triangle based on the definition of isosceles triangle.
If the hypotenuse and an acute angle of a right triangle are congruent to the hypotenuse and an acute angle of another right triangle then the two triangles are congruent. We are given AB AE and BC DE. Triangles ABC and DEF have the following characteristics.
Base angles in an isosceles triangle are congruent based on the isosceles triangle theorem so ABE AEB. Sides h and l are congruent. Hypotenuse-Acute HA Angle Theorem.

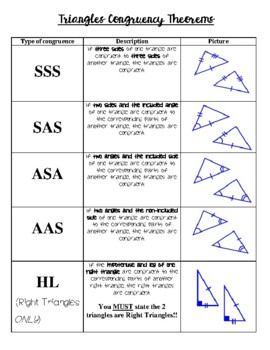
Triangle Congruence Theorem Teaching Resources Tpt

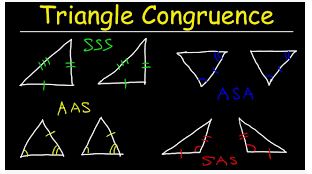
Comments
Post a Comment